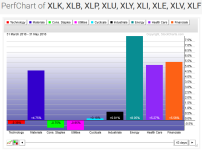
Sektorrotaion - ein interessantes und sehr weitläufiges Thema
Ich mache hier mal einen Thread dafür auf. Man hätte es auch in das Thema Intermarket Analyse integrieren können.
Als Literatur dazu kann man die Bücher von Murhpy wärmstens empfehlen.
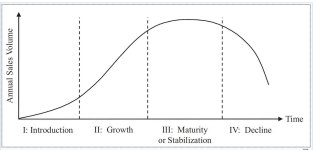
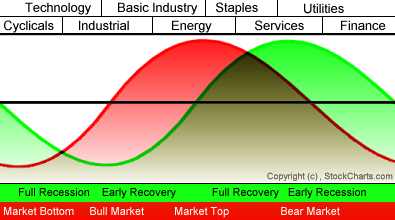
Hier eine gute Grafik mit den verschiedenen Sektoren aufgeteilt in die Marktzyklen, wo sie die anderen Sektoren outperformen:
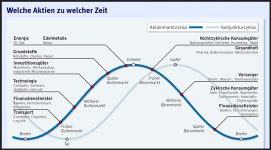
Quelle: FAZ
Wie eingangs schon erwähnt ist die Sektorenrotation ein sehr weitläufiges Thema. Ich werde hier sicher nicht alles wissenswerte darüber abdecken können. Erstens weil es schlicht zu viel wäre und zweitens weil ich mich selbst noch zuwenig detailliert damit auskenne. Wenn also jemand etwas dazu beitragen kann, wäre das herzlich willkommen. Ich fange mal an mit der Beschreibung aus Wikipedia:
Ich mache hier mal einen Thread dafür auf. Man hätte es auch in das Thema Intermarket Analyse integrieren können.
Als Literatur dazu kann man die Bücher von Murhpy wärmstens empfehlen.
Hier eine gute Grafik mit den verschiedenen Sektoren aufgeteilt in die Marktzyklen, wo sie die anderen Sektoren outperformen:

Quelle: FAZ
Wie eingangs schon erwähnt ist die Sektorenrotation ein sehr weitläufiges Thema. Ich werde hier sicher nicht alles wissenswerte darüber abdecken können. Erstens weil es schlicht zu viel wäre und zweitens weil ich mich selbst noch zuwenig detailliert damit auskenne. Wenn also jemand etwas dazu beitragen kann, wäre das herzlich willkommen. Ich fange mal an mit der Beschreibung aus Wikipedia:
Sector rotation is a term normally applied to stock market trading patterns.[1] In this context, a sector is understood to mean a group of stocks representing companies in similar lines of business.
For example, an investor or trader may describe the current market movements as favoring basic material stocks over semiconductor stocks by calling the environment a sector rotation from semiconductors to basic materials.
Investors may use Exchange Traded Funds (ETFs) to buy a diversified portfolio of stocks in various sectors and market segments and manage the portfolio according to ETF Rotation strategies.
Concept
A sector rotation theory says a number of things. First, whatever sector is hot (has done well recently) should continue to outperform. Second, these sectors will eventually rotate so that whatever was once out of favor will be in favor. Third, these movements are somewhat predictable. and connected with the business cycle.
Sources
Much description of sector rotation is taken from Intermarket Analysis by John Murphy.
Sector Rotation Models exist primarily to help investors identify and participate in new trending sectors of the stock market. A sector rotation investment strategy is not a passive investment strategy like indexing, and requires periodic review and adjustment of sector holdings. Tactical asset allocation and sector rotation strategies require patience and discipline, but have the potential to outperform passive indexing investment strategies.
An example of a sector rotation theory would be:
Leading
This includes stocks like consumer cyclicals and financial companies. These would do well when the market is at bottom.
In-line
This includes stocks like technology and telecommunication. These should go up more than the overall market in the main part of a bull market.
Lagging
This includes stocks like energy companies. These would do well when the market is at top.
Contrarian
This includes consumer staples. These should do least bad in a bear market.
Note that this is sectors relative to the overall market. It is expected that, during a bear market, all stocks will go down some.
Connection with other markets
The primary driver of sector rotation is the variability of currency values (inflationary, disinflationary, or deflationary) and interest rates. As the economy expands, demand for raw materials creates inflationary pressures, which in turn prompt higher interest rates, which increase the value of the currency, which reduces the competitiveness of a country's exports as the currency causes them to cost more to other countries. This final stage causes the economy to contract, reducing demand for raw materials, which creates deflationary pressures, which in turn prompt lower interest rates, which decrease the value of the currency, which increases the competitiveness of a country's exports—creating a new market cycle. The relative strength of commodities, bonds, currencies, and stocks shift in this changing monetary climate in a somewhat predictable manner.
Quelle: https://en.wikipedia.org/wiki/Sector_rotation